Cálculo del Radio Terrestre
El primer científico que obtuvo la medida del radio de la Tierra fue Eratóstenes (cerca del año 250 antes de Cristo). Él se dio cuenta de que mientras en la ciudad de Siena, Egipto (hoy Asuán) el Sol estaba directamente sobre la cabeza del observador en el mediodía del solsticio de verano, en Alejandría (ciudad ubicada a 5000 estadios = 800 km hacia el norte de Siena) la sombra de un obelisco formaba un ángulo de 7º 12´ en el mismo instante. ¿Cómo hizo Eratóstenes con estos datos para calcular el radio de la Tierra?

Veamos:
- Si en Siena el sol está justo sobre la cabeza del observador, entonces un obelisco en esta ciudad no hace sombra en ese instante.
- Si en Siena el sol está justo sobre la cabeza del observador, entonces un obelisco en esta ciudad no hace sombra en ese instante.
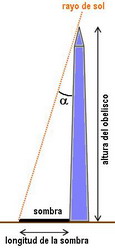
- Al mismo tiempo, en Alejandría los rayos del sol forman un ángulo α = 7º 12' con la vertical. Este dato se obtiene midiendo la sombra del obelisco (el obelisco forma un ángulo de 90º con su sombra en el piso):
tan (α) = longitud de la sombra / altura del obelisco
donde tan (α) es la tangente del ángulo α. (Fig. 1)
- Entre Siena (Asuán) y Alejandría hay aproximadamente 800 kilómetros
Nota: Originalmente Eratóstenes midió esta distancia usando el estadio egipcio como unidad (1 estadio = 185 metros), sin embargo, la longitud del estadio olímpico griego (estadio ático) es de 192 metros, por lo que existe cierta controversia sobre el valor realmente empleado y la exactitud del resultado obtenido.
En cuanto a cómo obtuvo el dato de la distancia entre las ciudades hay tres hipótesis: tomó la distancia estimada por las caravanas que comerciaban entre ellas; lo obtuvo en la Biblioteca de Alejandría; o calculó la distancia valiéndose de un regimiento de soldados que diera pasos de tamaño uniforme. Finalmente fijó 5000 estadios.
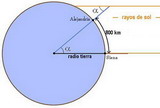
- Con estos datos y usando las herramientas trigonométricas ya estamos en condiciones de calcular el radio de la Tierra: (Fig. 2)
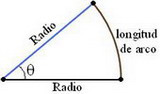
Trigonometría: La longitud de un arco sobre una circunferencia determinado por un ángulo θ, es igual al radio de la circunferencia multiplicado por el valor de θ expresado en radianes.
longitud de arco = Radio * θ (rad)
Radián: unidad estándar de medida de ángulos (180º = ¶radianes = 3,141592654 radianes)
- Para obtener el radio de la Tierra sólo hay que hacer esta cuenta: (Fig. 3)

Nota: Este método tiene un pequeño error debido a que las ciudades no se encuentran sobre el mismo meridiano, hay 5º de diferencia en longitud entre ellas.