El Boletín Radio@stronómico es una publicación trimestral, donde se incluyen noticias
relacionadas con la Astronomía y más específicamente la Radioastronomía. Es un
vehículo de comunicación que nos permite dar a conocer las novedades y actividades
desarrolladas en el Instituto.
A partir del número 11 el Boletín cuenta con su número de ISSN. El International Standard Serial Number (ISSN) es un número internacional normalizado que se asigna a las publicaciones periódicas, o sea a todas aquellas publicaciones que aparecen a intervalos regulares o irregulares de tiempo, y a las que comunmente se las conoce como revistas. Este número identifica a la publicación en forma única y se tramita a través del Centro Argentino de Información Científica y Tecnológica (Caicyt). Es importante para nosotros seguir trabajando para hacerles llegar nuestro Boletín. Desde ya estamos agradecidos y los instamos a comunicarse con nosotros para plantearnos cualquier consulta o sugerencia. 
|
Durante el mes de mayo el IAR recibió la visita del Prof. Dr. Hansjörg Kutterer, Director del Bundesamt für Kartographie und Geodäsie (BKG) de Alemania y Dr. Hayo Hase, Director del Observatorio Geodésico Integrado Transportable (TIGO, por sus siglas del inglés, Transportable Integrated Geodetic Observatory).
Como resultado de esta visita surgieron tratativas entre CONICET y la Bundesamt für Kartographie und Geodäsie (BKG), para instalar dentro del predio del IAR el mencionado observatorio TIGO. Para ello se le solicitó a nuestro Instituto un estudio del nivel de interferencias electromagnéticas (RFI, del inglés Radio Frequency Interference) presentes en el IAR, el que se llevó a cabo durante los meses de junio y julio.
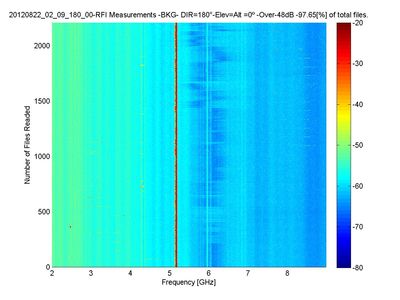
El equipo para realizar esta campaña denominado "Monitor de Interferencias de RF, RFI" está ubicado a 14mts de altura sobre el nivel del piso, tiene una cobertura espacial de 360° en pasos de 45°, cubriendo el rango de frecuencias desde 2GHz hasta 9Ghz con una ganancia de sistema de aproximadamente 75dB teniendo la capacidad de detectar señales de hasta -110dBm en los terminales de la antena, siendo asimismo capaz de observar en dos polarizaciones lineales (horizontal y vertical).
Como resultado de esta primera campaña el Director de TIGO visitó el IAR durante el mes de Agosto para realizar una serie de medidas complementarias con un nuevo instrumento provisto por BKG de Alemania.
Estas medidas que cubren un espectro mayor en frecuencia y con mayor sensibilidad ayudarán a determinar y caracterizar el nivel de interferencias electromagnéticas presentes en el IAR.
Más información: Monitoreo de Interferencias de RF (RFI)
|
- ¿Podrías contarnos cuál es tu área de especialización?
Pienso que la especialización está vinculada con actividades a quienes he dedicado más tiempo. Durante mis últimos 25 años tuve la suerte trabajar constantemente en proyectos vinculados al método de la medición con interferometría en líneas de base muy largas o VLBI (Very Long Baseline Interferometry).
Al inicio durante mis estudios universitarios trabajé en el análisis de datos VLBI, y después en el proyecto de iniciar mediciones VLBI en la base O'Higgins en Antárctica (1990-1993). He trabajado en la puesta en marcha del observatorio geodésico integrado transportable TIGO (Transportable Integrated Geodetic Observatory) en Wettzell, Alemania (1994-2001). Durante los últimos 10 años he tenido a mi cargola gerencia del Observatorio Geodésico TIGO en Concepción, Chile. Estuve también involucrado en la especificación técnica del Twin Telescope Wettzell, dos radiotelescopios de última generación para la geodesia (2006-2008). - ¿En qué institución desarrollas tu trabajo?
Mi empleador es la Oficina Federal de Cartografía y Geodesia de Alemania BKG (Bundesamt für Kartographie und Geodäsie). Esta oficina está subordinada al Ministerio Federal del Interior de Alemania. Como funcionario de esta institución tenemos responsabilidad de contribuir a la geodesia global con datos de nuestros observatorios en Alemania, Antárctica y actualmente en Chile.
- Nos gustaría saber cuál es la actividad concreta que has venido a desarrollar durante esta semana en el IAR.
La actividad consiste en realizar mediciones en el espectro electro-magnético entre 2 a 18 GHz con el fin de saber, si el sitio de IAR es apto para futuras mediciones VLBI para la geodesia y astrometría.
Hemos encontrados algunas "estrellas" terrestres, que tenemos que monitorear para entender su posible impacto a las observaciones de quasares utilizados en VLBI.
- ¿Te has sentido cómodo en nuestro país?
Mi impresión de Argentina es muy variada. Hay cosas que me gustan y otras que no me gustan. En general he sentido muy cómodo en conversaciones con argentinos, con las comidas finas y abundantes y con la belleza del entorno de algunos partes del país que he visitado. Después de cada visita a Argentina estuve saliendo con nuevas impresiones. Valoro mucho el sistema de educación gratuita (como en Alemania), el buen desarrollo turístico con muchas informaciones libres y el altruismo y solidaridad entre la gente.
- ¿Tenés futuros planes de retorno?
Mis próximas vacaciones las pasaré en Buenos Aires en septiembre para conocer más de la capital y sus habitantes.
Seguramente voy a volver al IAR, aún no tengo una fecha agendada. - Nos gustaría que nos cuentes cómo es un día de tu vida en Alemania. ¿Tenés algún Hobby o pasatiempo?
Salí de Alemania en el año 2001, por lo cual no sé cómo responder a mi vida en Alemania...
Cuando tengo tiempo para mí, practico natación master competitiva, me gusta trabajar con herramientas, por ejemplo mis dos bicicletas, o con madera y hago muebles. También me gusta leer y observar. Me encantó tomar fotos estéticas y buscar los motivos en todo el mundo. - ¡Muchas gracias Hayo!
|


Como todos los años en el mes de setiembre la Asociación Argentina de Astronomía (AAA) convoca a científicos nacionales y extranjeros para participar de este evento, el más importante a nivel nacional en esta área. Esto permite comunicar resultados, intercambiar ideas, desarrollar nuevos proyectos y acceder a los últimos avances logrados en Astronomía.
Este año la reunión se llevó a cabo entre los días 17 al 21 de septiembre, en la ciudad de Mar del Plata, organizada por el nuestro Instituto.
El personal del IAR presentó los siguientes trabajos: Charlas invitadas
1. Estrellas fugitivas y su impacto en el medio interestelar
Paula Benaglia Presentaciones orales
1. Burbujas infrarrojas: Gas molecular y polvo interestelar asociado a S21-24
E. Cappa, J. Vasquez, C. Kobulnicky, M. Rubio, G. A. Romero 2. Gas molecular asociado a IRAS 10361-5830
M. M. Vazzano, J. Vasquez, C. E. Cappa, G. A. Romero, M. Rubio 3. Black holes and accretion in strong f(r)-gravity
G. E. Romero, D. Pérez, S. E. Pérez Bergliaffa Presentaciones Murales
1. Energetics of nearby stellar bow shocks
Paula Benaglia 2. HD 112364: un sistema binario SB2
Corti, Mariela A. 3. Formación estelar inducida en la cáscara molecular G126.1–0.8–14
S. Cichowolski , M. E. Ortega , L. A. Suad, E. M. Arnal 4. X-ray structures from outflowing YSOs interacting with the ISM
M. Orellana, R. Bonito, J. López-Santiago, J. F. Albacete-Colombo 5. Estudio multifrecuencia del ob jeto candidato a YSO IRAS10349-5824
J. Vasquez, C. Cappa, G. Romero, M. Rubio 6. Estudio cinemático comparativo de 3 galaxias locales ricas en HI
J. Saponara, V. Lefranc, P. Benaglia, I. Andruchow, B. Koribalski 7. Compact Stars in R-Squared Gravity
Federico García, Florencia A. Teppa Pannia, Mariana Orellana, Gustavo E. Romero 8. Is there a Central Compact Object within G290.1–0.8
F. García, J. A. Combi, J. F. Albacete-Colombo, G. E. Romero, F. Bocchino, J. López-Santiago
9. Observaciones en el óptico de Blazares del Hemisferio Norte: Resultados de una larga campaña
Marchesini, E. J., Zibecchi, L., Andruchow, I., Cellone, S. A., Combi, J. A., Romero, G. E., Martí, J., Luque-Escamilla, P., Muñoz-Arjonilla, A. J., Sánchez-Sutil, J. R. 10. The Cherenkov Telescopes Array: status and perspectives
M. Clementina Medina 11. Detección en rayos-X de una protoestrella de gran masa
C. S. Peri, J. López-Santiago, J. F. Albacete-Colombo 12. Efectos de teorías de gravedad con dimensiones extra sobre un flujo de neutrinos ultra-energéticos de origen cósmico
M. M. Reynoso, O. A. Sampayo, G. E. Romero 13. Proyecto LLAMA: Caracterización de Alto Chorrillo
F. A. Bareilles, R. Morras, F. P. Hauscarriaga, E. M. Arnal 14. Aplicación de técnicas de análisis de redes sociales (ARS) y de co-ocurrencia de palabras en la determinación de frentes de investigación
C. E. Boeris Más información: 55º Reunión anual de la Asociación Argentina de Astronomía
|
El premio Carlos M. Varsavsky es uno de los tres premios destinados a reconocer y promover la actividad de investigación y desarrollo de la astronomía y la astrofísica en la República Argentina creados por la Asociación Argentina de Astronomía (A.A.A.).
Este premio se entrega cada dos años a la mejor tesis doctoral realizada en Argentina sobre un tema de astronomía o astrofísica, que haya sido defendida en una Universidad Nacional durante el período inmediato anterior.
El premio Carlos M. Varsavsky consiste en una medalla conmemorativa y un diploma, los cuales son entregados durante la correspondiente Reunión Anual de la A.A.A.. El ganador recibe, además, una invitación para realizar una presentación plenaria sobre el tema de su tesis en la misma reunión, estando sus gastos cubiertos por la A.A.A. Complementariamente, recibirá una suma de dinero proporcionada por la familia del Dr. Varsavsky que le posibilitará atender a una reunión internacional de su especialidad durante el año inmediato posterior a la entrega del premio.
La Dra. Vila desarrollo su Tesis sobre el tema "Radiative models for jets in X-ray binaries", dirigida en su ejecución por el Dr. Gustavo E. Romero. La defensa de la Tesis se llevo a cabo en la Universidad de Buenos Aires (UBA) en el mes de marzo del corriente.
La divulgacion de esta clase de logros es muy importante para una institución como el IAR, pues ademas del prestigio institucional que implica, sirve como atractivo para que estudiantes avanzados de Astronomia piensen en desarrollar sus actividades en el IAR.
|
Se llama a concurso abierto de antecedentes para cubrir dos cargos en la Carrera del Personal de Apoyo a la Investigación y Desarrollo de CONICET con lugar de trabajo en el Instituto Argentino de Radioastronomía.
 Un Profesional para tareas de diseño, desarrollo y mantenimiento preventivo y correctivo en el sector de mecánica. Un Profesional para tareas de diseño, desarrollo y mantenimiento preventivo y correctivo en el sector de mecánica. Descripción de las actividades:
- Llevar a cabo la dirección y planificación de los trabajos de diseño y desarrollo mecánico.
- Realizar análisis estructural y de transferencia de calor en sistemas mecánicos y aquellos que integran componentes mecánicos, electrónicos e informáticos. - Encargarse de la definición de los conceptos básicos en las diferentes líneas técnicas de las tareas. - Efectuar el seguimiento y evaluación concerniente a las tareas que se desarrollen en las áreas de mecánica y de electromecánica. - Realizar el mantenimiento preventivo y correctivo de equipos mecánicos, eléctricos y electrónicos en el laboratorio y los montados en los planos focales de las antenas de 30 metros de diámetro. - Redactar informes técnicos. - Brindar capacitaciones en el área de su desempeño. - Mantener el orden en el espacio físico donde se desempeña. - Cumplir las normas en Seguridad e Higiene Laboral y dirigir su implementación en la Unidad. - Brindar apoyo a las distintas áreas del Instituto. Requisitos para los postulantes:
- Graduado universitario en Ingeniería Mecánica.
- Experiencia mínima de 3 años en las tareas mencionadas. - Experiencia comprobable mínima comprobable de 3 años en análisis estructural y de transferencia de calor aplicando análisis de elementos finitos. - Experiencia mínima de 3 años en el manejo de CAD de la especialidad - Autocad, SolidWorks, Catia y ANSYS (deseable) para realizar las tareas de desarrollo mecánico y los análisis estructurales y de transferencia de calor. - Conocimientos en Seguridad e Higiene Laboral. - Competencias asociadas a realización de informes escritos, análisis de información y realización de indicadores. - Conocimiento oral y escrito del Idioma Inglés a nivel "intermediate" (excluyente). - Capacidad de transmisión de conocimientos. - Disponibilidad para viajes dentro y fuera del país. - Disponibilidad para realizar tareas en altura (torres y antenas parabólicas de gran diámetro). - Muy buena predisposición para trabajar en equipo dentro de un ambiente exigente. - Ser argentino nativo, o naturalizado. - El cargo a cubrir se encuadra en el régimen establecido por Ley 20464 para el personal de apoyo a la investigación y desarrollo de CONICET. - Los interesados deben cumplir con los requisitos establecidos en la Ley Marco de Regulación de Empleo Público Nacional, Ley 25164 y su Dec. de Empleo Reglamentario N°1421/02.  Un Técnico para diseño y desarrollo de antenas y alimentadores de antenas para uso terrestre y aeroespacial Un Técnico para diseño y desarrollo de antenas y alimentadores de antenas para uso terrestre y aeroespacial Descripción de las actividades:
- Realizar el diseño, desarrollo, seguimiento y evaluación relacionados con Antenas y Redes pasivas de Radiofrecuencia en las bandas de frecuencia L, S, C, X, Ku, K y Ka, con especial énfasis en antenas de uso satelital.
- Llevar a cabo el diseño y desarrollo de redes de distribución de potencia de RF. - Efectuar la medición de parámetros de antenas: ganancia, patrón de radiación y parámetros de dispersión. - Definir los conceptos básicos de las diferentes líneas técnicas de las tareas. - Redactar informes técnicos. - Mantener el orden en el espacio físico donde se desempeña. - Realizar las tareas atendiendo las normas de seguridad establecidas por la Unidad. Requisitos para los postulantes:
- Secundario completo. Preferentemente estudiante avanzado en Ingeniería Electrónica o en Ingeniería en Comunicaciones.
- Experiencia mínima comprobable de 3 años en tareas afines. - Poseer muy buen manejo de los siguientes programas de simulación: HFSS, Ansoft Designer y FEKO (excluyente). - Conocimientos de diseño y simulación 3D de antenas para uso espacial y de laboratorio (excluyente). - Poseer muy buen manejo de las aplicaciones de diseño asistido (CAD) AUTOCAD o CATIA (preferentemente) y del paquete Matlab. - Poseer buen manejo de instrumental de RF: Analizador de espectro, Analizador vectorial de redes, generadores de señal, en el rango de 1 a 40GHz. - Competencias asociadas a realización de informes escritos, análisis de información y realización de indicadores. - Conocimiento de escritura y lectura en inglés a nivel "Intermediate" - Muy buena predisposición para trabajar en equipo dentro de un ambiente exigente. - Ser argentino nativo, o naturalizado. - El cargo a cubrir se encuadra en el régimen establecido por Ley 20464 para el personal de apoyo a la investigación y desarrollo de CONICET. - Los interesados deben cumplir con los requisitos establecidos en la Ley Marco de Regulación de Empleo Público Nacional, Ley 25164 y su Dec. de Empleo Reglamentario N°1421/02. En ambos casos deberán enviar:
- Curriculum vitae
- Nota de elevación dirigida al Director del Instituto, Dr. E. M. Arnal - Fotocopia del DNI (hojas 1 y 2) - Fotocopia del/los certificado/s de estudios y de toda otra documentación de respaldo que considere apropiada. Presentación:
Personalmente en sobre cerrado entregado en la Secretaría del Instituto Argentino de Radioastronomía. El sobre debe ser dirigido al Comité de Selección concurso Personal de Apoyo, o por correo postal en sobre cerrado dirigido a Instituto Argentino de Radioastronomia, Comité de Selección concurso Personal de Apoyo, C.C. No. 5, 1894 Villa Elisa, Argentina.
Los postulantes que cumplan con los requisitos de inscripción y sean preseleccionados por el Comité de Selección serán citados telefónicamente, o por e-mail, para una entrevista personal.
Fecha de apertura: 10 de septiembre de 2012
Fecha de cierre: 10 de octubre de 2012 a las 12:00 horas. Los postulantes que cumplan con los requisitos de inscripción y sean preseleccionados por el Comité de Selección serán citados telefónicamente o por e-mail para una entrevista personal.
|
Se incorpora al IAR el 20 de agosto, como Investigadora Asistente de la Carrera del CONICET, bajo la direccion del Dr. Gustavo E. Romero, a cuyo grupo pertenece.
Trabajará en CTA, simulaciones, y desarrollo de tecnología, manteniendo fuertes vinculos con las instituciones francesas. |

|
Por el Dr. Gustavo E. Romero
1- Teoría y realidad
El objetivo de una teoría física es representar la realidad (p. ej., Bunge, 1967). Una premisa básica de la ciencia es que hay "cosas" en el Mundo y que esas cosas tienen propiedades (esta es una hipótesis ontológica). Las propiedades pueden ser representadas por funciones matemáticas y por otros objetos abstractos inventados por los seres humanos conforme a reglas coherentes (p. ej., Bunge, 2006). El valor de las funciones y la estructura de los objetos matemáticos de la teoría están restringidos por ecuaciones y condiciones matemáticas que representan leyes físicas, es decir, restricciones al espacio posible de los estados de las cosas. Cuando cambian las propiedades de las cosas, decimos que ocurre un evento. Un evento se puede especificar por un par ordenado representaciones de estados de una cosa (ver Bunge, 1977). Cada estado esta caracterizado por una colección de valores de funciones de estado. Ciertamente la caracterización de una cosa no es única. El modelo específico de una cosa depende de aquellos aspectos de la realidad que la teoría aborda. La sucesión de eventos (o procesos) que ocurren con una cosa forma su historia.
Toda teoría física se refiere a algún tipo de entidad concreta. La existencia de esas entidades es supuesta por la teoría. Si la teoría es exitosa, ganamos confianza en la existencia de las entidades. Si la teoría fracasa, podemos considerar a las entidades postuladas sólo como hipótesis exploratorias que pueden ser abandonadas. Por ejemplo, el modelo estándar de la física de partículas supone la existencia de dos tipos diferentes de cuantones: leptones y quarks. Estos interactúan por medio de partículas llamadas bosones. La existencia de los bosones W+- y Z0 fue una hipótesis de trabajo del modelo de interacción electrodébil hasta el descubrimiento de las partículas en experimentos a finales de la década de 1970. Ahora, estos bosones son considerados tan reales como los fotones. Los taquiones, por el contrario, han sido actualmente descartados por causa tanto de razones teóricas como por la falta de evidencias observacionales. Otras partículas, como el bosón de Higgs, continúan hipotéticas, aunque plausibles hasta el momento.
Los tipos de objetos que las teorías físicas suponen como elementos del mundo pueden cambiar a medida que evoluciona nuestro conocimiento. Desde las plantas, los animales y los planetas hasta las partículas elementales y las estrellas de quarks, nuestra visión del universo puede cambiar, alterando nuestras nociones de lo que creemos que existe, de cómo son las cosas y cómo se relacionan.
2- El modelo de variedad del espacio-tiempo
La relatividad general es la teoría del espacio, el tiempo y la gravitación formulada por Albert Einstein en noviembre de 1915 (Einstein, 1916). Se trata de una teoría extraordinariamente exitosa que pasó muchas pruebas, sobre todo en los límites de campo débil o bajas energías. Es una teoría altamente compleja, donde el campo gravitacional esta descripto a través de la curvatura del espacio-tiempo. Las ecuaciones de campo son diez ecuaciones diferenciales no lineales en los coeficientes del tensor métrico del espacio-tiempo. La teoría alcanza su máximo desarrollo cuando es expresada independientemente de las coordenadas en el lenguaje de la geometría diferencial abstracta. En esa formulación, conocida como modelo de variedad del espacio-tiempo (p. ej., Hawking & Ellis, 1973; Joshi, 1993). La teoría puede ser aplicada en los contextos más variados, desde objetos compactos con gravedad fuerte hasta el universo entero.
El concepto básico de esa formulación de la relatividad general es el del espacio-tiempo, introducido por Hermann Minkowski, en 1908 (Minkowski, 1909). El espacio-tiempo puede ser definido como la suma ontológica [1] de todos los eventos que ocurren en todas las cosas. No se trata de un mero conjunto, que es un objeto matemático (es decir, una ficción), sino de una propiedad relacional emergente de todas las cosas. Todo lo que ocurrió, todo lo que ocurre, todo lo que va a ocurrir es apenas un elemento del espacio-tiempo.

Figura 1: Hermann Minkowski
Como para toda propiedad física, podemos representar el espacio-tiempo como alguna estructura matemática. La estructura matemática y la propiedad representada no deben ser confundidas: la correspondencia nunca es perfecta, permanece siempre provisoria. El modelo de variedad del espacio-tiempo adopta la siguiente estructura matemática:
El espacio-tiempo puede ser representado por una variedad real C∞-diferenciable y cuadridimensional.
Una variedad cuadridimensional real es un conjunto que puede ser completamente cubierto por subconjuntos cuyos elementos estén en correspondencia uno en uno con subconjuntos de R4. Cada evento es representado por un punto en la variedad (el inverso no es necesariamente cierto). Cada elemento de la variedad representa un evento. Adoptamos 4 dimensiones porque parece suficiente dar 4 números reales para localizar un evento y eso puede hacerse independientemente de la geometría intrínseca de la variedad. Si existe más de una caracterización de un evento, siempre podemos encontrar una ley de transformación entre los diferentes sistemas coordenados. Esta es una propiedad básica de las variedades.
Si queremos calcular distancias entre dos eventos, necesitamos más estructura en la variedad: necesitamos una estructura geométrica. Podemos conseguirla introduciendo un campo tensorial métrico gab para determinar distancias. La separación infinitesimal entre dos elementos de la variedad, que representan dos eventos del espacio-tiempo, es dada por:
ds2 = gabdxadxb. (1)
El espacio-tiempo, entonces, es enteramente representado por un par ordenado (M, g) donde M es la variedad y g es el campo tensorial métrico. En la relatividad general, la métrica del espacio-tiempo esta determinada por la energía-impulso de los sistemas físicos a través de las ecuaciones de campo de Einstein. La propia métrica representa el potencial gravitacional y sus derivadas determinan las ecuaciones de movimiento a través de la conexión afín de la variedad. En forma simplificada, las ecuaciones de Einstein pueden escribirse como:
Gab(gab)= k Tab, (2)
donde el lado izquierdo es puramente geométrico y el derecho representa a los sistemas físicos. Así, las ecuaciones relacionan la métrica del espacio-tiempo con la materia, y permiten explicar la gravitación como mera curvatura del espacio-tiempo.
Como ocurre con cualquier otra teoría física, el modelo de variedad del espacio-tiempo supone algunas entidades que son representadas matemáticamente. La premisa básica aquí es la existencia de lo que es representado por los puntos de la variedad: la totalidad de los eventos, los cambios de todas las cosas.

Figura 2: Albert Einstein.
Como la variedad es cuadridimensional, un proceso, o incluso toda la historia de una cosa tridimensional, puede ser reprensado por un objeto cuadridimensional (p. ej., Heller, 1990; Balashov, 2010). Si bien la experiencia humana con el cambio pudo ser usada para inspirar el concepto de variedad, una vez adoptado, es posible describir el espacio-tiempo desde un punto de vista cuadridimensional, donde no existe cambio global. Una alteración del espacio-tiempo exigiría una dimensión extra que en él no esté incluida. Eso, a su vez, implicaría que el espacio-tiempo es una cosa con una propiedad relacional emergente que debería ser mediada por la dimensión extra o 'meta-tiempo'. No existe razón física para introducir tal ontología. Y si alguien estuviera dispuesto a pagar el precio para hacerlo, se sigue inmediatamente una regresión infinita, porque el 'súper espacio-tiempo' de 5 dimensiones podría cambiar, exigiendo más dimensiones extra. La inflación ontológica se tornaría inadmisible.
Series de cambios y procesos irreversibles de cosas físicas son descriptos por asimetrías, características intrínsecas, del espacio-tiempo. La dinámica es el resultado de la comparación de diferentes porciones del espacio-tiempo. El 'presente' no es una cosa que se mueve. Es solamente un concepto, una clase de eventos. Todo eso conforma la llamada ontología del universo en bloque (p. ej., Smart, 1963; Balashov, 2010). Esa visión también fue expresada, de forma bastante poética, por Hermann Weyl (1949):
El mundo objetivo simplemente es, no transcurre. Solamente desde el punto de vista de mi conciencia, recorriendo la línea de la vida de mi cuerpo, es que una sección de ese mundo ve la vida como una imagen efímera en el espacio que cambia continuamente con el tiempo.
3 - El universo parmenidiano
Parmenides nació y vivió en Elea, una ciudad en la costa occidental del sur de Italia, desde fines del siglo VI hasta mediados del siglo V a.C. Escribió un poema titulado Sobre lo que es. Casi toda la primera parte del poema y fragmentos de la segunda sobrevivieron gracias a Simplicius, que copió parte del texto en el siglo VI d.C. en su comentario sobre la Física de Aristóteles.
La primera parte del poema se llama El camino de la verdad. Esa obra contiene el primer ejemplo conocido de un sistema deductivo aplicado a la realidad física. Parménides no se contento sólo con dar su visión del mundo. Sustentó su interpretación del mundo por la deducción lógica a partir de lo que consideraba premisas evidentes. Afirmaba que no hay cambio, no hay un convertirse, no hay un llegar a ser. La realidad se muestra inmutable, eterna, inmóvil, perfecta y única. Sólo existe una cosa: el mundo. Su monotonía es absoluta. Lo que creemos es un mundo cambiante es sólo el resultado de ilusión y engaño.

Figura 3: Parménides de Elea
Las premisas del argumento de Parménides pueden ser escritas de la siguiente forma:
-Lo que es, es.
-Lo que no es, no es.
Así, nada puede llegar a ser a partir de lo que no es, porque 'lo que no es' no es cosa alguna. Creatio ex nihilo no tiene sentido. El cambio es imposible, ya que, para Parménides, el cambio es la ocupación del espacio vacío, pero no puede haber 'espacio vacío'. La realidad debe ser, entonces, un bloque inmutable.
Muchos siglos después de Parménides, con el surgimiento de las teorías de campo, quedó claro que el cambio puede ocurrir aún en un universo lleno: el cambio no requiere un espacio vacío. Una perturbación en un campo que ocupe todo el universo es un cambio.
El concepto de cambio es imprescindible en el modelo de variedad del espacio-tiempo. Pero una vez que la geometría de la variedad es determinada por un campo tensorial su estructura esta fija. El universo es representado por el triplete (M, g, T), donde T es el campo tensorial que representa las propiedades (energía e impulso) de las cosas. Puntos de la variedad representan eventos, pero no hay eventos o cambios afectando el espacio-tiempo como un todo. El espacio-tiempo cuadridimensional, matemáticamente representado por la variedad, es inmutable, eterno, inmóvil, único, así como el universo de Parménides. Lo que llamamos procesos irreversibles son descriptos por asimetrías en la variedad. Los objetos que constituyen el universo son cuadridimensionales. Tienen 'partes temporales', así como partes espaciales. De esta forma, el niño que un día fui es solamente una parte de un ser mayor, yo, que es cuadridimensional. Lo que llamamos 'nacimiento' y 'muerte' son apenas fronteras temporales de ese ser. El cambio aparece sólo cuando consideramos porciones tridimensionales de objetos cuadridimensionales. En las palabras de Max Tegmark:
El tiempo es la cuarta dimensión. El paso del tiempo es una ilusión. Tenemos esa ilusión de un mundo cambiante, tridimensional, aunque nada cambia en la unión cuadridimensional del espacio y del tiempo de la teoría de la relatividad de Einstein. Si la vida fuese una película, la realidad física sería un DVD entero: cuadros pasados y futuros existen tanto como el presente [2].
No parece injusto llamar a esa interpretación del espacio-tiempo una visión parmediana del mundo. Parménides, podemos decir, esta de vuelta con una venganza, en 4 dimensiones.
4 - Objeciones
Recientemente, Mario Bunge (2011) criticó duramente la interpretación del modelo de variedad del espacio-tiempo arriba descripto. La idea central de su argumentación es la siguiente:
Si puntos en una grilla del espacio-tiempo son identificados como eventos, en vez de decir que representan eventos posibles, el devenir desaparece. Pero eso es un absurdo: usted aún esta vivo, sus bisnietos aún no nacieron, la próxima crisis económica aún esta por venir, el sol aún no estalló, y así sucesivamente. Novedades ocurren objetivamente todo el tiempo, aún cuando el origen del tiempo sea convencional. Como la conclusión neo-parmenidiana es totalmente falsa, su premisa debe ser falsa también. ¿Cual era la premisa? Que puntos del espacio-tiempo = eventos, en lugar de puntos del espacio-tiempo representan eventos. O sea, el problema en cuestión es una falacia semántica: la de identificar el mapa con el territorio, el retrato con el retratado, el diagrama con la red, el modelo con su referente.
Sostengo que no hay una falacia semántica aquí. Como queda claro a partir de las definiciones dadas arriba, el espacio-tiempo no tiene 'puntos'. El espacio-tiempo fue definido como una colección de eventos. Es una propiedad relacional emergente de todas las cosas cambiantes. La variedad, que es ciertamente un concepto matemático, representa el espacio-tiempo, y los elementos de la variedad representan eventos. No concuerdo con que el espacio-tiempo sea una cosa, conforme sostienen los substantivistas (p. ej., Nerlich, 1994). Sostengo que el espacio-tiempo es una propiedad emergente de todas las cosas materiales. Se trata de la mismísima posición sostenida por Bunge (1977) y desarrollada por Perez-Bergliaffa et al. (1998), entre otros. El 'retrato' es el modelo de variedad, el 'retratado' es el espacio-tiempo, y el espacio-tiempo emerge de cosas cambiantes. Por lo tanto, la premisa ontológica del modelo de variedad del espacio-tiempo es la de que las cosas cambian, algo que Bunge probablemente no va a negar. Pero el propio espacio-tiempo no puede cambiar, al menos que aceptemos un tiempo multidimensional, no estando las dimensiones extras incluidas en el espacio-tiempo (ver argumentos contra el tiempo multidimensional en Bunge, 1958).
La emergencia del espacio-tiempo a partir de cosas básicas cambiantes también es esencial para los fundamentos de la gravedad cuántica (p. ej., Rovelli, 2004). Si las cosas se relacionan discontinuamente, el propio espacio-tiempo debería exhibir características cuánticas.

Figura 4: Mario Bunge
Otro argumento de Bunge es:
... la noción de que el tiempo es sólo una dimensión geométrica, en conjunto con las otras tres (o siete), es falsa también, como es demostrado por el papel privilegiado que tiene en las ecuaciones de movimiento. Por ejemplo, la ecuación de Hamilton dp/dt = δH/δx no tiene contrapartida espacial. Del mismo modo, las condiciones de frontera, tan importantes en la mecánica del continuo y en la mecánica cuántica, no tienen contrapartidas temporales.
Esas afirmaciones se basan en una interpretación incorrecta del modelo de la variedad. El tiempo no está en pie de igualdad con las otras dimensiones, ya que la métrica del espacio-tiempo es representada por un campo tensorial de traza -2, y no 4. La variedad es localmente lorentziana, no euclidiana, y por lo tanto representa correctamente el papel distintivo del tiempo. Una mera 'espacialización' del tiempo es inconsistente con nuestro conocimiento actual de la naturaleza. Además de esto, pueden encontrarse inconsistencias en el presentismo defendido por Bunge: en un universo con una velocidad constante y finita para la propagación de las interacciones, la simultaneidad no es absoluta como en un espacio newtoniano (Einstein, 1905) y el pasado y el futuro de eventos no conectados casualmente son relativos a un sistema de referencia. Eso no significa que algunos eventos existan con respecto a un sistema y no a otro. Las restricciones impuestas a un sistema de referencia físico son epistemológicas, no ontológicas. La existencia es invariante sobre transformaciones generales de coordenadas. Los eventos que llamamos 'futuros' son tan reales como aquellos que llamamos 'pasados' (p. ej., Putnam, 1967).
En cuanto a las condiciones de borde, sus contrapartidas temporales son las llamadas condiciones iniciales. Las condiciones de borde en el espacio-tiempo deben ser fijadas en 4 dimensiones para hacer predicciones. No debemos confundir el poder predictivo de nuestras teorias con el determinismo ontológico. Este es una doctrina metafísica: la doctrina de que todos los eventos existen, independientes de nuestra capacidad de conocerlos o predecirlos. El modelo de variedad del espacio-tiempo es onotológicamente determinista, aunque sea compatible con la indeterminación epistémica.
Puede ser que el modelo de espacio-tiempo sea, en última instancia, incorrecto. Todas las representaciones de la realidad son meras aproximaciones imperfectas. Pero los problemas del modelo no son semánticos. Están mas relacionados probablemente con la aplicabilidad del concepto de variedad para representar eventos en la escala de Planck.
5 - El río de Heráclito
Es común oponer a las ideas de Parménides de realidad inmutable la visión heraclitiana de que 'todo fluye'. Esa opinión, ciertamente, no se basa en los fragmentos existentes, sino que en la interpretación de Platón, presentada en su Cratilo (DK 22A6 [3]):
Todas las cosas se mueven y nada queda, y, asemejando cosas existentes con el fluir de un río, él dice que no se puede entrar dos veces en el mismo río.
El origen de esto parece estar en el fragmento de Heráclito DK 22B12:
Para los que entran siempre en los mismos ríos, fluyen aguas siempre diferentes.

Figura 5: Heráclito de Éfeso.
En el Teeto, Platón además atribuye a Heráclito la idea de que todas las cosas están siempre cambiando en todos los aspectos. Como ya fuera indicado por McKirahan (1994), Platón está considerando no el pensamiento de Heráclito, sino algunas elaboraciones extremistas hechas mucho más tarde por heraclitianos o tal vez hasta por Cratilo. Los fragmentos de Heráclito parecen enfatizar la estabilidad a través de cambio y no un COSMOS en mutación (κóσμος). Es más, un COSMOS basado solamente en el cambio, sin estabilidad o ARMONÍA (αρμονια), es una contradicción en términos, una contradicto in adjecto: seria el CAOS (Χαος). La idea más importante en los fragmentos de Heráclito es que existe un LOGOS (λóγς) en el COSMOS, una especie de principio general que se aplica a todo. Si permanecemos fieles a los fragmentos existentes, vemos que Heráclito declara que la estabilidad es alcanzada a través del cambio continuo. Si un río no fluye, si no 'contiene' cambio, no es un río: es un lago. Es sólo a través del cambio que el río alcanza su estabilidad. Lo mismo se puede extender a todas las cosas. Fragmento DK 22B84a:
Cambiando, está en reposo.
Heráclito, además, comparte algunas inquietudes espitemológicas y ontológicas con Parménides, como se muestra en DK 22B59 y DK 22B123, respectivamente:
Escuchando no a mí, sino al LOGOS, es sabio concordar que todas las cosas son una sola.La naturaleza gusta de esconderse.
Ofrezco al lector la sugerencia de que el antagonismo ontológico entre Parménides y Heráclito, normalmente mencionado por tantos autores, es el resultado de una tradición doxográfica que se origina en Platón. No hay mucho en el poema de Parménides, ni en los fragmentos existentes de Heráclito, que apoyen una oposición frontal. El COSMOS (el espacio-tiempo en una visión más moderna) puede ser inmutable y, no obstante, estar formado por cosas cambiantes. Tal como el río de Heráclito.
6 - Conclusión: el tiempo no pasa
No predico la espacialización del tiempo. Sostengo, meramente, que el espacio-tiempo, una propiedad emergente de todas las cosas, no puede cambiar. No hay nada respecto de lo cual el espacio-tiempo pueda cambiar, ya que lo incluye todo. Procesos irreversibles son representados por asimetrías de la variedad que proporciona un modelo para el espacio-tiempo. El espacio-tiempo puede ser modelado porque forma parte de la realidad física, como cualquier otra propiedad relacional. El tiempo no fluye. No puede fluir porque no es una cosa. El tiempo no pasa. Nosotros, sí.
Apéndice
Presentismo
Presentismo
El presentismo, doctrina defendida por Bunge, puede definirse como la tesis de que sólo el presente es real. Más precisamente (ver Crisp, 2010):
Presentismo. Es siempre el caso en que, para cada x, x es presente.
El 'presente' parece referirse a un dado instante de tiempo. El tiempo es normalmente representado por un continuo de una dimensión real. Es claro que la elección del origen de coordenadas, cuando adoptamos una métrica para el tiempo, es convencional. Los eventos señalizados por diferentes instantes, en cambio, no lo son. ¿Qué evento es presente? ¿Cuándo es el presente? La respuesta para ser "ahora". 'Ahora', como sugerí en otro lugar, parece ser una clase de eventos que se relacionan con un dado estado cerebral (Romero 2011, ver también Grünbaum, 1973). Si esta hipótesis es correcta, el 'presente' es una construcción del cerebro basado en su interacción con una clase de cosas cambiantes que lo afectan. El 'presente' no es una cosa que se desplaza del pasado hacia el futuro. Todo proceso cerebral conciente tiene su propio presente.
Algunas personas piensan en el presente como un tipo de frontera entre lo que existió (y de alguna forma desapareció) y lo que no existe: el futuro. Las cosas surgen de la nada, existen durante un período, y después desaparecen para siempre. Eso viola lo que probablemente sea el principio más básico de la ciencia, un principio introducido por Parménides: nada surge de la nada. El presentismo implica que todo surge de la nada, todo el tiempo, y desaparece de vuelta en la nada después de un intervalo de tiempo indivisible. Hasta Heráclito, me atrevo a decir, quedaría aterrorizado.
El presentismo es también incompatible con la física moderna. Consideremos dos eventos: yo digito esta línea (evento e1) y una supernova explota en la galaxia M83 (e2). Esos eventos pueden ser considerados simultáneos para algunos 'observadores' (o sea, cuando los medimos en algún sistema de referencia), o relacionados por 'e1 anterior a e2' en otro referencial, o 'e1 es posterior a e2' en aún otro referencial. El hecho es que ambos eventos existen, sean presente o no para algunas personas. De la misma forma, Parménides existe en alguna región del espacio-tiempo, que cubre Elea y parte de la Grecia antigua entre, digamos, 515 y 450 a.C. Y, durante algún tiempo, compartió su presente con Zenón. Yo existo más allá de la región del espacio-tiempo ocupada por Parménides. Nunca nos encontraremos. Pero ambos somos parte del mismo espacio-tiempo. Me siento afortunado por eso.
Agradecimientos
Estoy muy agradecido al profesor Mario Bunge por discusiones, charlas y consejos a lo largo de ya más de 20 años. Agradezco a Santiago Perez Bergliaffa, a Valenti Bosch-Ramon y a Daniela Pérez por comentarios valiosos sobre el texto original. María Victoria del Valle me ha brindado una valiosa ayuda en la traducción de este texto.
Referencias
Y. Balashov (2010). Persistence and Spacetime. Oxford: Oxford University Press.
M. Bunge (1958). On multi-dimensional time. British J. Phil. Sci. 9: 39.
M. Bunge (1967). Foundations of Physics. Berlin: Springer-Verlag.
M. Bunge (1977). Ontology I: The Furniture of the World. Dordrecht: Kluwer.
M. Bunge (2006). Chasing Reality. Toronto: University of Toronto Press.
M. Bunge (2011). Parmenides redux?, preprint.
T.M. Crisp (2003). Presentism. In: M.J. Loux and D.W. Zimmerman (Eds.), The Oxford Handbook of Metaphysics. Oxford: Oxford University Press (pp. 211-245).
E. Eaves (2008). What is Time?, in Forbes, February 29th.
A. Einstein (1905). Zur Electrodynamic bewegter Körper, Annalen der Physik 322, 891-321.
A. Einstein (1916). Die Grundlage der allgemeinen Relativitsätstheorie, Annalen der Physik 49, 769-822.
A. Grünbaum (1973). Philosophical Problems of Space and Time. Dordrecht: Reidel, 2nd ed.
S.W. Hawking, and G.F.R. Ellis (1973). The Large Scale Structure of Space-Time. Cambridge: Cambridge University Press.
M. Heller (1990). The Ontology of Physical Objects. Cambridge: Cambridge University Press.
P.S. Joshi (1993). Global Aspects in Gravitation and Cosmology. Oxford Clarendon Press.
R.D. McKirahan (1994). Philosophy before Socrates. Indianapolis Hackett Publishing Co.
H. Minkowski (1909). Lecture "Raum und Zeit, 80th Versammlung Deutscher Naturforscher (Köln, 1908)". Physikalische Zeitschrift 10, 75-88.
G. Nerlich (1994). The Shape of Space, Cambridge: Cambridge University Press.
S.E. Perez Bergliafa, G. E. Romero, and H. Vucetich (1998). Toward an axiomatic pregeometry of space-time, Int. J. Theor. Phys. 37, 2281-2298.
H. Putnam (1967). Time and Physical Geometry, The Journal of Philosophy 64, 240-247.
G.E. Romero, Brain and Cosmos, en prensa (2012).
C. Rovelli (2004). Quantum Gravity, Cambridge: Cambridge University Press.
J.J.C. Smart (1963). Philosophy and Scientifc Realism. New York: Routledge and Kegan Paul.
H. Weyl (1949). Philosophy of Mathematics and Natural Science. Princeton: Princeton
[1] Escribo suma ontológica y no 'agregación mereológica' porque no considero el espacio-tiempo como una cosa, ni como un individuo, pero, sí, como una propiedad emergente de
todas las cosas cambiantes. Ver Perez Bergliaffa et al. (1998).
[2] A partir de una entrevista de Eaves (2008).
[3] La notación se refiere a doxografia en H. Diels e W. Kranz, Die Fragmente de repente Vorsokratiker, 6ª ed., Berlín, 1951.
Sobre el autor:
Gustavo E. Romero es Doctor en Física por la Universidad Nacional de La Plata. Actualmente es Profesor Titular de Astrofísica Relativista en la Facultad de Ciencias Astronómicas y Geofísicas de la UNLP e Investigador Principal del CONICET, con lugar de trabajo en el Instituto Argentino de Radioastronomía. Dirige el Grupo de Astrofísica Relativista y Radioastronomía (GARRA), ha sido Profesor Visitante de las universidades de Barcelona, Paris VII, Campinas y Hong Kong, entre otras, e Investigador Visitante del Max-Planck-Institut für Kernphysik (Heidelberg), el Service d'Astrophysique (Saclay, Francia), el Instituto di Astrofísica Spaziale e Física Cósmica (IASF, Bologna, Italia), etc. Ha recibido los máximos premios a la investigación científica en Argentina: El Premio Bernardo Houssay del MCyT (único argentino en recibirlo en dos oportunidades), el Premio J.L. Sérsic de la Asociación Argentina de Astronomía y el Premio E. Gaviola de la Academia Nacional de Ciencias. Fue Presidente de la Asociación Argentina de Astronomía. También ha recibido varias distinciones internacionales, incluyendo dos menciones de honor de la Gravity Research Foundation. El Dr. Romero ha publicado más de 290 artículos sobre gravitación, astrofísica, filosofía y religión. Entre sus libros se destacan "¿Es Posible Viajar en el Tiempo?" (Ed. Kaicron, BsAs, 2010) e "Introducción a la Astrofísica Relativista" (Publicaciones de la Universidad de Barcelona, 2011). Actualmente es Sub-director de nuestro Instituto.

Gustavo E. Romero, en Éfeso.

Por Lic. Daniela Perez
El fin de una era
En la última entrevista dada por Albert Einstein, dos semanas antes de su muerte, recordó a los científicos que admiraba: Newton, Lorentz, Planck y Mach; junto con Maxwell, eran los únicos que Einstein consideraba como sus precursores.
James Clerk Maxwell nació en 1831 en Edimburgo, Escocia; estudió física y matemática en la Universidad de Edimburgo y Cambridge. Sus intereses eran diversos: la óptica, la naturaleza de los anillos de Saturno, hasta la poesía británica. Maxwell, sin embargo, se abocó especialmente al estudio de los fenómenos eléctricos y magnéticos.
A finales del siglo XIX se pensaba que las fuerzas de la naturaleza eran de tres tipos: gravitacional, eléctrica y magnética. La electricidad se caracteriza por la existencia de dos tipos de carga eléctrica, una positiva y otra negativa. Cargas del mismo signo se repelen y cargas de signo opuesto se atraen con una intensidad que varía con la distancia de la misma forma que la fuerza gravitacional.
La similitud entre la fuerza magnética y eléctrica ya había sido advertida por los griegos en la antigüedad. A principios del siglo XIX, Hans Christian Ørsted demostró que cargas eléctricas en movimiento generan un campo magnético. Otros experimentos conducidos por André-Marie Ampère, Michael Faraday, en el transcurso del mismo siglo, confirmaban la íntima relación entre estos dos campos.
En el año 1865, Maxwell fue el responsable de la unificación de estas dos fuerzas en lo que se llamó electromagnetismo. Las ecuaciones de Maxwell son la representación matemática de las propiedades físicas del campo electromagnético. Las manifestaciones del mismo, que anteriormente parecían desvinculadas, podían ser explicadas ahora en términos de una única teoría. Maxwell además predijo que la oscilación periódica de cargas eléctricas en movimiento produciría ondas electromagnéticas que se propagarían a la velocidad de la luz. Esto último fue comprobado por Heinrich Rudolf Hertz (1857-1894) 20 años después. Hertz fue el primero en detectar y generar ondas electromagnéticas en laboratorio. Este singular evento marcó el inicio de la era de las telecomunicaciones.
Al igual que sus contemporáneos, Maxwell pensaba que dado que las ondas electromagnéticas se propagan, deberían hacerlo en un medio, denominado éter; éste se caracterizaba por llenar todo el espacio, estar en reposo absoluto respecto a las estrellas fijas y por ser transparente al movimiento de la Tierra. Uno de los desafíos científicos más importantes en aquellos años era la demostración experimental de la existencia del mismo. En su artículo Ether, escrito para la novena edición de la Enciclopedia Britannica Maxwell explica entre otras cosas, sus infructuosos esfuerzos al tratar de detectar la influencia del arrastre del éter en el movimiento de la Tierra; concluye que estos efectos al ser muy pequeños en nuestro planeta son indetectables y que acaso mediante algún tipo de observación astronómica podría llegar a demostrarse la existencia de esta sustancia. En particular, sugiere el cálculo de la velocidad de la luz a partir de la observación de los eclipses de las lunas de Júpiter.
El 19 de marzo de 1879 Maxwell envía una carta de agradecimiento a David Peck Todd, Director del Nautical Almanac Office en Washington, por el envío de datos del Sistema Joviano. En ella se refiere a su artículo de la enciclopedia y remarca la imposibilidad de la detección del éter en experimentos que involucren a la Tierra. Esta carta fue escrita por Maxwell cuando le quedaban ocho meses de vida y Einstein sólo tenía cinco días. Luego de la muerte de Maxwell la carta fue reenviada a la secretaria de la Royal Society y posteriormente publicada en la revista Nature.
Un año y medio después, en agosto de 1881, apareció un artículo en la revista American Journal of Science cuyo autor era Albert Abraham Michelson. Nacido en Prusia (hoy Polonia) en 1852, Michelson vivió muy poco en su país natal: a los tres años de edad con sus padres emigró a Estados Unidos. A los 17 años ingresó en la Academia Naval de dicho país donde se destacaría más en ciencia que en la labor marítima. Su interés en el estudio de la determinación de la velocidad de la luz se remonta a su época de oficial. En 1879 deja su cargo de instructor científico en la Academia y mientras realizaba sus estudios en el laboratorio de Helmholtz en Berlín, lee por primera vez la carta de Maxwell de 1879. Siendo Michelson un conocido experto en las mediciones de la velocidad de la luz, comprende que Maxwell desconocía el alto grado de precisión con que podían hacerse dichos experimentos. En Berlín diseña el interferómetro; el experimento, sin embargo, fue realizado en el observatorio astrofísico cercano a Potsdam para evitar cualquier tipo de vibración urbana que pudiese afectar el resultado. En su artículo de agosto de 1881 Michelson concluye que no observó ninguna evidencia del 'viento de éter'.
Pocos científicos prestaron atención su trabajo. Hendrik Antoon Lorentz (1853-1928), sin embargo, encontró errores en el experimento y dudaba de la interpretación de los resultados. El experimento volvió a repetirse esta vez en colaboración con Edward Williams Morley en la Case School of Applied Science en Cleveland. Los resultados nuevamente demostraron que los efectos del éter sobre la velocidad de la luz eran nulos y la comunidad científica aceptó la validez de los mismos. En otras palabras, el experimento de Michelson-Morley evidenció la inconsistencia de la teoría dinámica de la luz vigente en el siglo XIX.
La teoría de campo electromagnético desarrollada por Maxwell fue ampliamente aceptada por sus contemporáneos. Ésta, sin embargo, no era invariante bajo las transformaciones de coordenadas introducidas por Galileo, lo cual era un gran problema para los científicos de aquellos años.
El concepto de transformación de coordenadas se refiere a cómo cambian las diferentes cantidades físicas medidas por observadores en movimiento relativo. Por ejemplo, si hay dos personas sentadas en un avión, la velocidad de una respecto a la otra, en el sistema de referencia fijo al avión, es cero. La velocidad, sin embargo, de cualquiera de ellas respecto a otra persona sentada en el jardín de su casa que observa el vuelo de la nave, es igual a la velocidad del avión tal como es registrada por el piloto en la cabina. Galileo introdujo una regla de adición simple que permite transformar las velocidades de un sistema de referencia a otro.
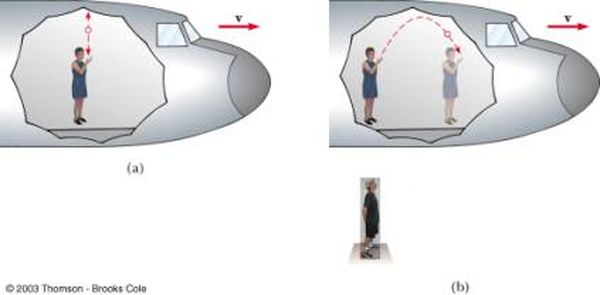 Figura 2. a) El pasajero del avión lanza hacia arriba una pelota; en su sistema de referencia la trayectoria de la pelota es vertical. b) Para un observador en Tierra, la nave se mueve a una velocidad v y debido al movimiento de ésta, la trayectoria de la pelota es parabólica.
Las transformaciones de Galileo se derivan del principio de relatividad: la representación de los fenómenos físicos es independiente de la posición y movimiento de los observadores; en otras palabras, la forma de las leyes que rigen el mundo físico no dependen del sistema de coordenadas usado para describirlo (una mera invención humana). La mecánica desarrollada por Newton es perfectamente compatible con las transformaciones de Galileo, pero no así la teoría electrodinámica de Maxwell: las leyes del electromagnetismo no son invariantes, esto es cambian de forma, al ser sometidas a una transformación de Galileo. Otro grupo de transformaciones, sin embargo, de carácter completamente diferente al de Galileo dejaban invariantes las ecuaciones de Maxwell, las hoy conocidas como 'transformaciones de Lorentz'.
Albert Einstein sentía una profunda admiración por Lorentz y decía no haber conocido a otro hombre con una personalidad tan armoniosa. Lorentz fue un físico matemático neerlandés que junto con George Francis FitzGerald (1851-1901) formuló la llamada contracción FitzGerald-Lorentz. En un trabajo publicado en 1889 en el American Journal of Science titulado 'The Ether and the Earth´s Atmosphere' FitzGerald explica de forma cualitativa que "... la longitud de los cuerpos materiales cambia al moverse a través del éter…". Como se explicará más adelante, esta formulación es pre-relativista ya que se sigue suponiendo la existencia del éter y los cambios de longitudes se consideran, en palabras de Einstein, objetivamente reales; es un cambio absoluto, no un cambio relativo respecto a un observador en reposo. Lorentz por su parte, inventó las transformaciones que llevan su nombre; éstas no sólo dejan invariantes las ecuaciones de Maxwell sino que reducen la contracción de FitzGerald-Lorentz a una consecuencia de las transformaciones de Lorentz.
Jules Henri Poincarè (1854-1912) fue indiscutiblemente uno de los precursores de Einstein. Éste último, sin embargo, jamás lo citó en sus trabajos. De la misma forma Poincarè sólo se refirió a Einstein en dos ocasiones. La primera en relación a la relatividad cuando las autoridades del Instituto Federal de Tecnología (ETH) de Zürich, le pidieron su opinión sobre Einstein, a quien pensaban ofrecerle un cargo de profesor. La segunda y última fue en relación al efecto fotoeléctrico. Tres meses después murió de forma inesperada a los 58 años de embolia. Einstein, dos meses antes de morir, dio su última opinión acerca de Poincarè: "Lorentz ya había reconocido que las transformaciones que llevan su nombre son esenciales para el análisis de las ecuaciones de Maxwell, y Poincarè profundizó este conocimiento aún más…"
Sólo un año antes de la aparición de la Teoría Especial de la Relatividad, en el International Congress of Arts and Science en St. Louis, Poincarè cuestiona la existencia del éter, objeta el concepto de velocidad absoluta y simultaneidad e intuye que acaso una nueva dinámica debe construirse donde la velocidad de la luz es el límite máximo para la velocidad de los cuerpos. Poincarè fue un visionario y el último "universalista" (después de Gauss) capaz de entender y contribuir en todos los ámbitos de la disciplina matemática.
Figura 3. Einstein y Lorentz fotografiados por Ehrenfest en la puerta de su casa en Leiden en 1921.
1905
En sus días de estudiante en el ETH, Einstein no se caracterizó por atender regularmente a clases; prefería estudiar aquellos temas de la física que pensaba eran relevantes. Por ejemplo, nunca se interesó por el curso Introducción a la Física Teórica dictado por uno de sus profesores, Weber, ya que lo creía un típico representante de la física clásica que simplemente ignoraba todo después de Helmholtz2 . No todos sus profesores pertenecían a la categoría de Weber: en varias ocasiones Einstein destacó como excelentes profesores de matemática a Adolf Hurwitz y Hermann Minkowski. Este último no guardaría un buen recuerdo de Einstein como alumno.
 Figura 4. Einstein junto a sus compañeros de clase en el ETH. Einstein disfrutó las libertades que tenía en su época de estudiante; hacía lo que quería hasta unos meses antes del 'detestable' período de exámenes; Marcel Grossmann, uno de sus grandes amigos, para ayudarlo le prestaba sus notas de los cursos 'bien escritas y meticulosamente organizadas'. En agosto de 1900, Einstein se graduó de Fachlehrer3 junto a otros tres estudiantes, quienes inmediatamente obtuvieron una posición como asistentes en el ETH. Él, sin embargo, estaba sin trabajo. Weber le había prometido un puesto académico y luego se desentendió del asunto, episodio que Einstein nunca terminó de perdonarle.
Dos años transcurrieron antes de su primer trabajo estable que fue como técnico de tercera clase en la oficina de patentes en Berna. Es notable que aunque Einstein estaba completamente apartado del ámbito académico, nunca dejó de pensar y trabajar en ciencia. En 1903 y 1904 publicó trabajos sobre los fundamentos de la mecánica estadística. Al año siguiente, en marzo, sobre la explicación del efecto-fotoeléctrico (por el que recibiría el premio Nobel de física de 1923). El 30 de abril completa su tesis doctoral sobre 'Una nueva determinación de las dimensiones moleculares'. Este trabajo es el más citado de la historia debido a que los resultados obtenidos tienen un rango muy amplio de aplicaciones: desde la industria de la construcción (el movimiento de las partículas de arena en las mezclas), la industria lechera (el movimiento de las micelas de caseína en la leche de vaca) hasta ecología (el movimiento de las partículas de aerosol en las nubes), por mencionar algunos ejemplos. El 11 de mayo envía para su publicación un artículo con la explicación del movimiento browniano (pequeños movimientos de partículas en suspensión de líquidos), donde demuestra la existencia de los átomos.
La Relatividad Especial nació luego de diez años de continua investigación y reflexión. Einstein, sin embargo, vislumbró las ecuaciones fundamentales de la teoría en poco menos de seis semanas.
Según relató Einstein, en aquel tiempo estaba seguro que las Ecuaciones de Maxwell eran correctas y debido a la llamada invariancia de la velocidad de la luz dichas ecuaciones tendrían que tener la misma forma en un sistema de referencia en movimiento uniforme. La invariancia de la velocidad de la luz, sin embargo, entraba en conflicto con la regla de adición de velocidades de la mecánica, esto es, las transformaciones de Galileo. Durante más de un año estuvo pensando en el problema.
Einstein cuenta en la conferencia de Kioto4: "Inesperadamente un amigo mío en Berna me ayudó. Ese fue un día muy hermoso cuando lo visité y comencé a hablarle de esta manera: 'Tengo una pregunta que me es muy difícil de entender. He venido aquí hoy para librar una batalla con ella'. Luego de mucha discusión, comprendí repentinamente el asunto. Al día siguiente lo volví a visitar y le dije sin saludarlo: 'Gracias. He resuelto completamente el problema"'.
Su amigo en Berna era Michele Besso, a quien conocía desde sus días de estudiante en Zürich y era además colega en la oficina de patentes desde 1904. Sólo a él le dedicó su trabajo titulado "Sobre la electrodinámica de los cuerpos en movimiento", recibido por la revista Annalen der Physik el 30 de junio de 1905. Este artículo fue la presentación original de la Teoría Especial de la Relatividad.
La nueva cinemática
"Mi solución era realmente del concepto del tiempo, esto es, que el tiempo no está absolutamente definido sino que hay una conexión inseparable entre el tiempo y la velocidad de la señal. Con estas concepciones, la extraordinaria dificultad anterior pudo ser resuelta. Cinco semanas después que reconocí esto, la presente teoría de la relatividad especial estaba completa". Con estas palabras Albert Einstein explicaba en la conferencia de Kioto que la nueva teoría surgió esencialmente del abandono de la mecánica clásica en la descripción de los fenómenos electromagnéticos.
Einstein, como ya hemos mencionado, creía en la 'verdad de las ecuaciones de Maxwell'. Éstas, sin embargo, no eran invariantes bajo las transformaciones de Galileo, esto es, cambiaban de forma respecto a diferentes sistemas de referencia. El gran paso que dio Einstein para resolver el problema fue mantener la electrodinámica de Maxwell y modificar la mecánica de Newton para que satisfaga la invariancia bajo transformaciones de Lorentz. La nueva teoría fue relativista, ya que contrariamente a la teoría absoluta de Newton, ciertos parámetros como la masa del cuerpo, pasaban a depender de la velocidad del cuerpo relativa a un cierto sistema de coordenadas. El concepto mismo de simultaneidad de dos eventos se vuelve relativo al sistema de referencia utilizado para describir los eventos. La Teoría Especial de la Relatividad implicó una nueva forma de pensar en física, ya que los conceptos más esenciales en nuestra descripción del mundo, tales como el espacio y el tiempo perdían su carácter 'absoluto'.
 Figura 5. Einstein y su amigo Michele Besso. El núcleo de la formulación de la nueva teoría está contenido en dos postulados. Los dos postulados de la teoría son:
1. El Principio de Relatividad: la formulación de las leyes de la física debe ser invariante bajo transformaciones de coordenadas entre sistemas inerciales.
2. El Principio de Constancia de la Velocidad de la Luz: la velocidad de la luz es la misma en todos los sistemas de referencia inerciales.
Un sistema inercial es un cuerpo cuya velocidad es constante respecto a todos los sistemas de la misma clase. Dado que la velocidad relativa entre todos estos sistemas no cambia, están libres de aceleración, y por lo tanto de las llamadas 'fuerzas no inerciales'; todos los días experimentamos éstas fuerzas: en el ascensor, cuando un automóvil o cualquier otro medio de transporte cambia su velocidad, por mencionar algunos ejemplos. La teoría se llamó 'especial' ya que está restringida a sistemas de referencias inerciales.
El aspecto más revolucionario de la teoría fue la desaparición de la simultaneidad absoluta. La duración de un intervalo de tiempo para un observador inercial (en movimiento rectilíneo y uniforme) no tiene porqué coincidir con la duración del mismo intervalo para otro observador. El tiempo se vuelve relativo al sistema de referencia y por lo tanto al estado de movimiento del sistema. ¿Cómo es que siempre hemos observado que la duración de un intervalo de tiempo es la mismo independientemente de la velocidad del observador? La respuesta es que los efectos relativistas comienzan a ser significativos para velocidades mayores a 100000 km/s, esto es para velocidades comparables con la velocidad de la luz.
Estamos aún muy lejos de poder construir vehículos que se muevan a velocidades cercanas a la de la luz: la nave más rápida diseñada en la historia fueron las sondas espaciales Helios, construidas y operadas por la República Federal de Alemania y la NASA entre 1974 y mediados de la década de los ochenta; tenían por misión estudiar el Sol y el medio interestelar contenido dentro de la órbita de Mercurio. Estas naves alcanzaron velocidades de 252792 km/h o equivalentemente, 70.22 km/s, esto es el 0.000234 de la velocidad de la luz. La mecánica newtoniana, por lo tanto, describe perfectamente aquellos fenómenos físicos que no involucren velocidades relativistas, como es el caso del movimiento de cuerpos en la Tierra, o hasta el momento, vehículos construidos por el hombre.
La desaparición de la simultaneidad absoluta implica que para objetos que se mueven a velocidad muy altas, comparables a la de la luz, el tiempo se dilata respecto a objetos que permanecen en reposo. El tiempo medido por el reloj de un dado observador se llama 'tiempo propio' de ese observador. A un lapso de tiempo propio breve, puede corresponder un lapso de tiempo externo largo si el observador se mueve a velocidades comparables a la velocidad de la luz (denotada por el símbolo c). La relación entre el tiempo propio t y el tiempo externo t se expresa en forma matemática como:
donde γ es el llamado factor de Lorentz, un número mayor a 1, que depende de la velocidad. A medida que la velocidad aumenta, a igual tiempo propio corresponden tiempos externos cada vez mayores.
La verificación del fenómeno de 'dilatación temporal' implica la observación y medición de objetos con velocidades cercanas a la de la luz. Como se ha mencionado, se está aún lejos de poder construir vehículos que se muevan a esas velocidades; el universo, sin embargo, es el mejor laboratorio para testear muchas teorías de la física y en particular ha posibilitado verificar el fenómeno de dilatación temporal mediante la observación de partículas sub-atómicas relativistas. La existencia de dichas partículas se conoce desde la década de 1910 cuando en una serie de vuelos en globo, Victor Hess (1883-1964) descubrió que la Tierra se encuentra inmersa en un mar de radiación cósmica. Esta radiación está mayormente formada por partículas llamadas muones creadas por la interacción de rayos cósmicos (partículas muy energéticas provenientes del espacio) con los átomos de la alta atmósfera. En el sistema de referencia propio del muon, sin embargo, sólo viven alrededor de dos microsegundos, tiempo insuficiente para poder estar siquiera a kilómetros de nuestras cabezas. La razón de que muones llegan a la superficie del planeta es la dilatación del tiempo predicha por la relatividad especial: el tiempo de vida de los muones aumenta cuando es medido desde un sistema de referencia terrestre.
 Figura 6. Sonda Helios A en la cima del cohete Titan IIIE Centauro. Cortesía NASA. Einstein y la relatividad especial después de 1905
Luego de la publicación de sus trabajos en Relatividad Especial, Einstein estaba decepcionado: según cuenta su hermana Maja, éste pensaba que inmediatamente aparecerían en el Annalen der Physik duras críticas y gran oposición a sus revolucionarias ideas. En las ediciones posteriores de la revista, sin embargo, no había mención alguna a sus trabajos. Einstein, al poco tiempo, recibe una carta enviada por un profesor en Berlín, donde se pedía aclaración sobre algunos puntos de la teoría. El joven científico comprende que su trabajo no había pasado desapercibido, más aún porque el Profesor Max Planck, el científico más importante de la época, era quien le había escrito; el interés de Planck por la Relatividad Especial hizo que ésta comenzará a hacerse conocida y fuese un tópico de discusión en el ambiente científico.
A partir de 1906, Einstein dejó de ser un total desconocido que trabajaba en sus momentos libres en diversos problemas de la física: varios científicos viajaron a Berna para discutir con él sobre la teoría. Von Laue, asistente de Planck, fue uno de los primeros y aseguró haber quedado completamente sorprendido al ver que aquel joven era el padre de la Relatividad Especial (Einstein tenía en aquel momento 27 años).
Varios científicos hicieron importantes aportes a la teoría luego de su publicación. Hermann Minkowski (1864-1909) fue quien introdujo los conceptos de espacio-tiempo, cono de luz, línea de mundo, además de formular la teoría en lenguaje tensorial. Las primeras reacciones de Einstein frente a este nuevo formalismo matemático fueron de completo rechazo: llegó a calificar el trabajo de Minkowski como "erudición superflua". Más tarde su opinión cambiaría drásticamente: en 1912 adoptó el método tensorial y en 1916 reconoció que gracias a Minkowski, fue mucho más fácil la transición de la Relatividad Especial a la Relatividad General
 Figura 7. Max Planck y Albert Einstein, 1928. En 1907, mientras escribía un artículo acerca de las consecuencias de la Relatividad Especial, Einstein comprendió que todos los fenómenos podían ser descriptos en términos de la Relatividad Especial, excepto para aquellos sistemas que estuviesen acelerados. Pensaba en particular en sistemas inmersos en un campo gravitatorio. Dado que todos los cuerpos, independientemente de su naturaleza, se aceleran de la misma forma, el estado de movimiento entre observadores en caída libre sería el de reposo. El postulado del Principio de Relatividad, entonces, tendría que extenderse a sistemas que, entre ellos, estén en movimiento no uniforme.
Einstein vislumbró las limitaciones de su teoría. El camino hacia la Relatividad General había comenzado.
Referencias
- Luminet, J. P. (2010). Black Holes. Black Holes. Cambridge: Cambridge University Press.
- Pais, A. (2010). Subtle is the lord. The science and the life of Albert Einstein. Oxford: Oxford University Press.
- Romero, G. E. (2010). Es posible viajar en el tiempo? Buenos Aires: Editorial Kaicron.
Notas
1- Palabras pronunciadas el 6 de abril de 1922 en la Sociéte Française de Philosophie, durante una reunión para discutir sobre la Relatividad Especial y General.
2- Hermann Ludwing Ferdinand von Helmholtz (1821-1894): fue un médico y físico alemán, conocido por sus trabajos en termodinámica y electrodinámica.
3- Fachlehrer es un maestro especializado en una dada asignatura para la enseñanza en colegios secundarios. En el caso de Einstein, las asignaturas eran matemática y física.
Sobre el autor
|
El Área de Divulgación del IAR continúa su labor llevando a cabo las tradicionales visitas guiadas por el Instituto. Estas visitas guiadas para establecimientos educacionales consisten en proyección de material audiovisual, charla explicativa y recorrida por sus instalaciones.
Los días de atención son los viernes, en dos turnos:
Tel/Fax: (0221) 425-4909 y (0221) 482-4903 E-mail : difusion@iar.unlp.edu.ar
Por razones de organización, las visitas guiadas se restringen al periodo comprendido entre principios de abril y principios de diciembre de cada año.
Para mayor información: Visite nuestra página web: http://www.iar.unlp.edu.ar/divulgacion.htm

|
En esta sección encontrará artículos publicados en diversos medios acerca de las distintos actividades del IAR y su gente.
- Entregan premio en homenaje a distinguido astrónomo - Código Mar del Plata (21-09-2012)
|
Selección de contenidos y diagramación: Lic. Claudia Boeris C.C. Nelva Perón Asesoramiento científico: Dirección: Camino Gral. Belgrano Km 40 (Parque Pereyra Iraola) Berazategui - Prov. de Buenos Aires - ARGENTINA Dirección Postal: Casilla de Correo No. 5 1894 -Villa Elisa Prov. de Buenos Aires - ARGENTINA Teléfonos y FAX: Tel: (0221) 482-4903
Tel/Fax: (0221) 425-4909 Correo electrónico 
|
Año 1 Nº 1 - Junio de 2003
Año 1 Nº 2 - Septiembre de 2003 Año 1 Nº 3 - Diciembre de 2003 Año 2 Nº 4 - Marzo de 2004 Año 2 Nº 5 - Junio de 2004 Año 2 Nº 6 - Setiembre de 2004 Año 2 Nº 7 - Diciembre de 2004 Año 3 Nº 8 - Marzo de 2005 Año 3 Nº 9 - Junio de 2005 Año 3 Nº 10 - Setiembre de 2005 Año 3 Nº 11 - Diciembre de 2005 Año 4 Nº 12 - Marzo de 2006 Año 4 Nº 13 - Junio de 2006 Año 4 Nº 14 - Setiembre de 2006 Año 4 Nº 15 - Diciembre de 2006 Año 5 Nº 16 - Marzo de 2007 Año 5 Nº 17 - Junio de 2007 Año 5 Nº 18 - Setiembre de 2007 Año 5 Nº 19 - Diciembre de 2007 Año 6 Nº 20 - Marzo de 2008 Año 6 Nº 21 - Junio de 2008 Año 6 Nº 22 - Setiembre de 2008 Año 6 Nº 23 - Diciembre de 2008 Año 7 Nº 24 - Marzo de 2009 Año 7 Nº 25 - Junio de 2009 Año 7 Nº 26 - Setiembre de 2009 Año 7 Nº 27 - Diciembre de 2009 Año 8 Nº 28 - Marzo de 2010 Año 8 Nº 29 - Junio de 2010 Año 8 Nº 30 - Setiembre de 2010 Año 8 Nº 31 - Diciembre de 2010 Año 9 Nº 32 - Marzo de 2011 Año 9 Nº 33 - Junio de 2011 Año 9 Nº 34 - Setiembre de 2011 Año 9 Nº 35 - Diciembre de 2011 Año 10 Nº 36 - Marzo de 2012 Año 10 Nº 37 - Junio de 2012 
|
©Instituto Argentino de Radioastronomía - (2012)